Batch Informed Trees (BIT*): Informed asymptotically optimal anytime search
Sahasrajit Anantharamakrishnan*, Shankara Narayanan Vaidyanathan*, Drake Moore*, Thejaswini Goriparthi*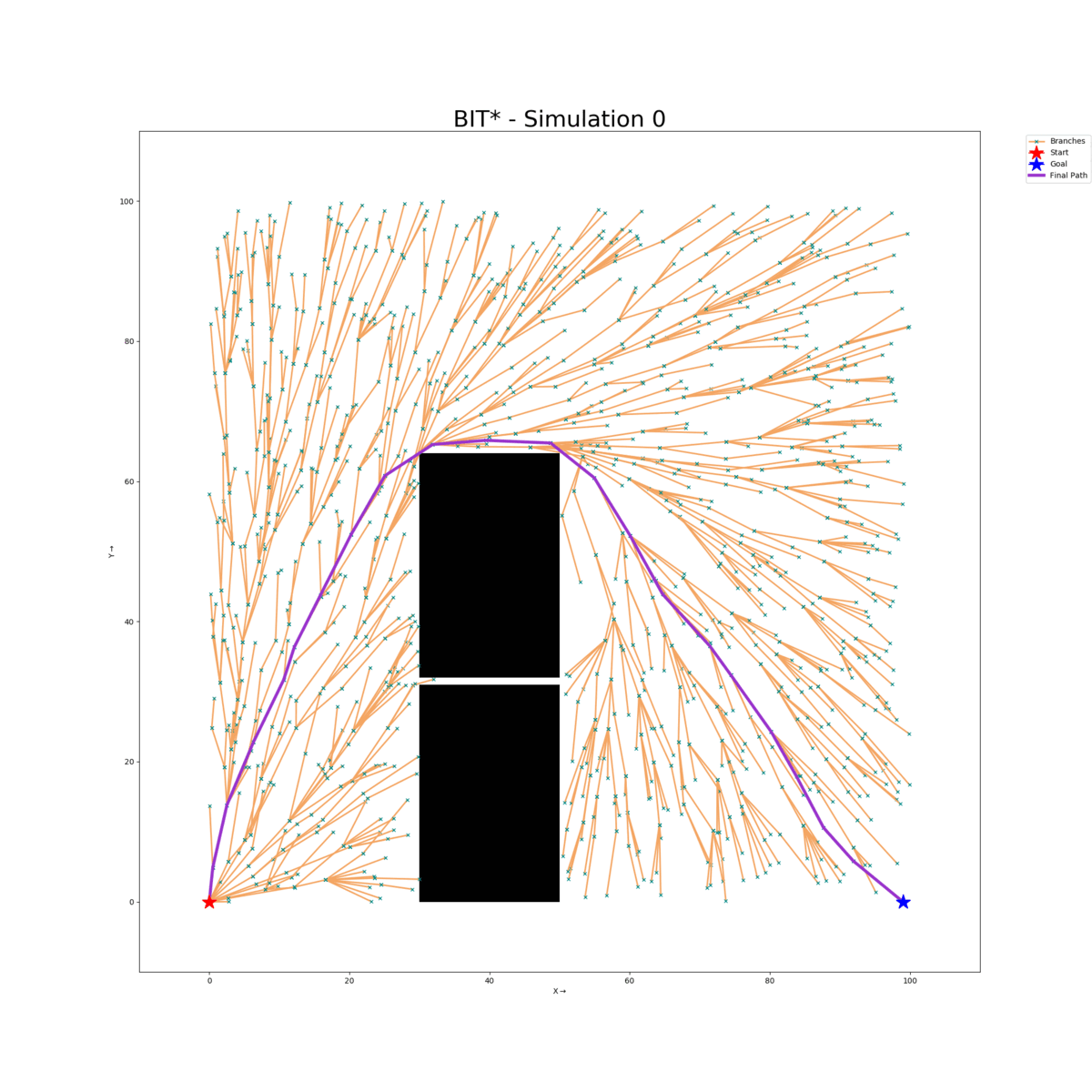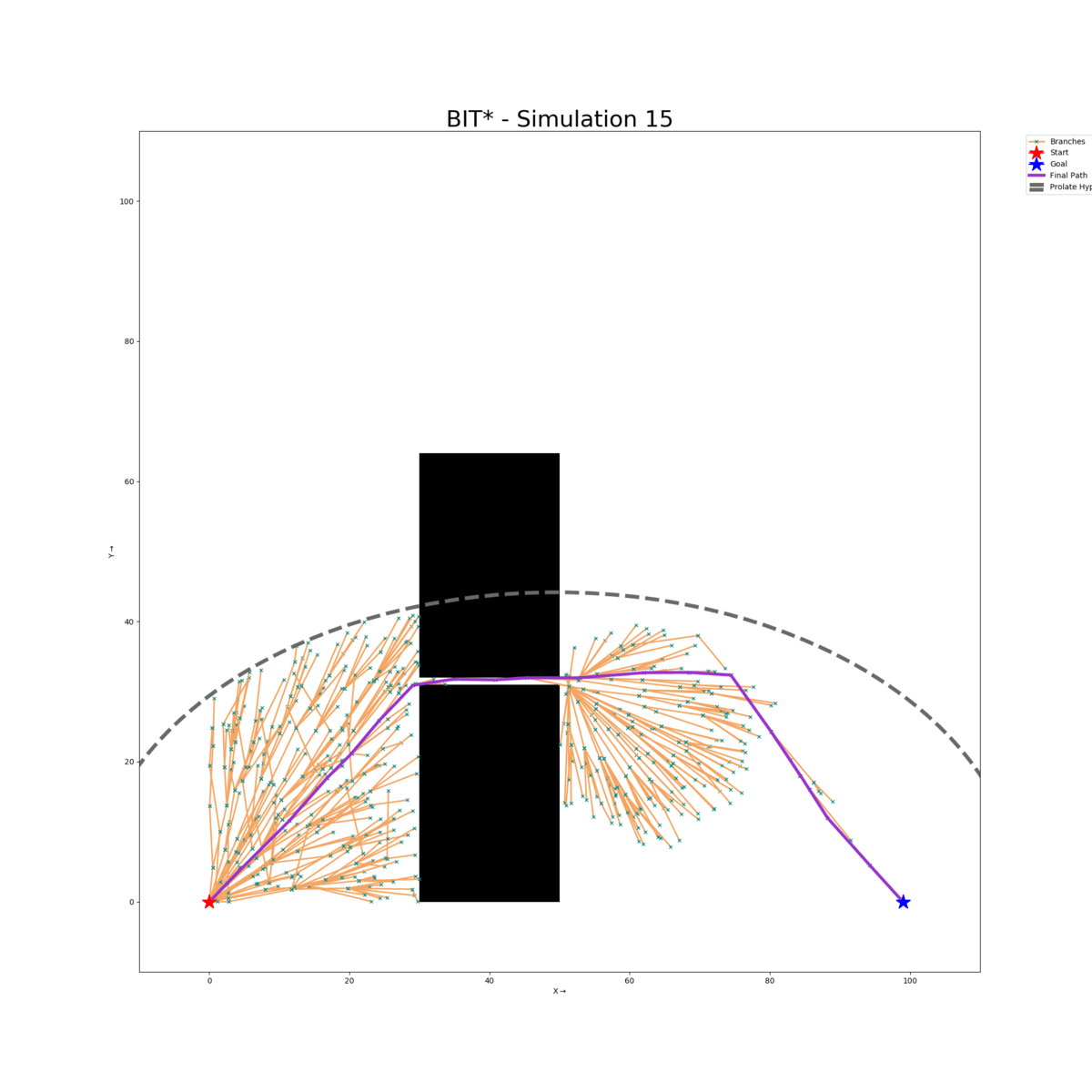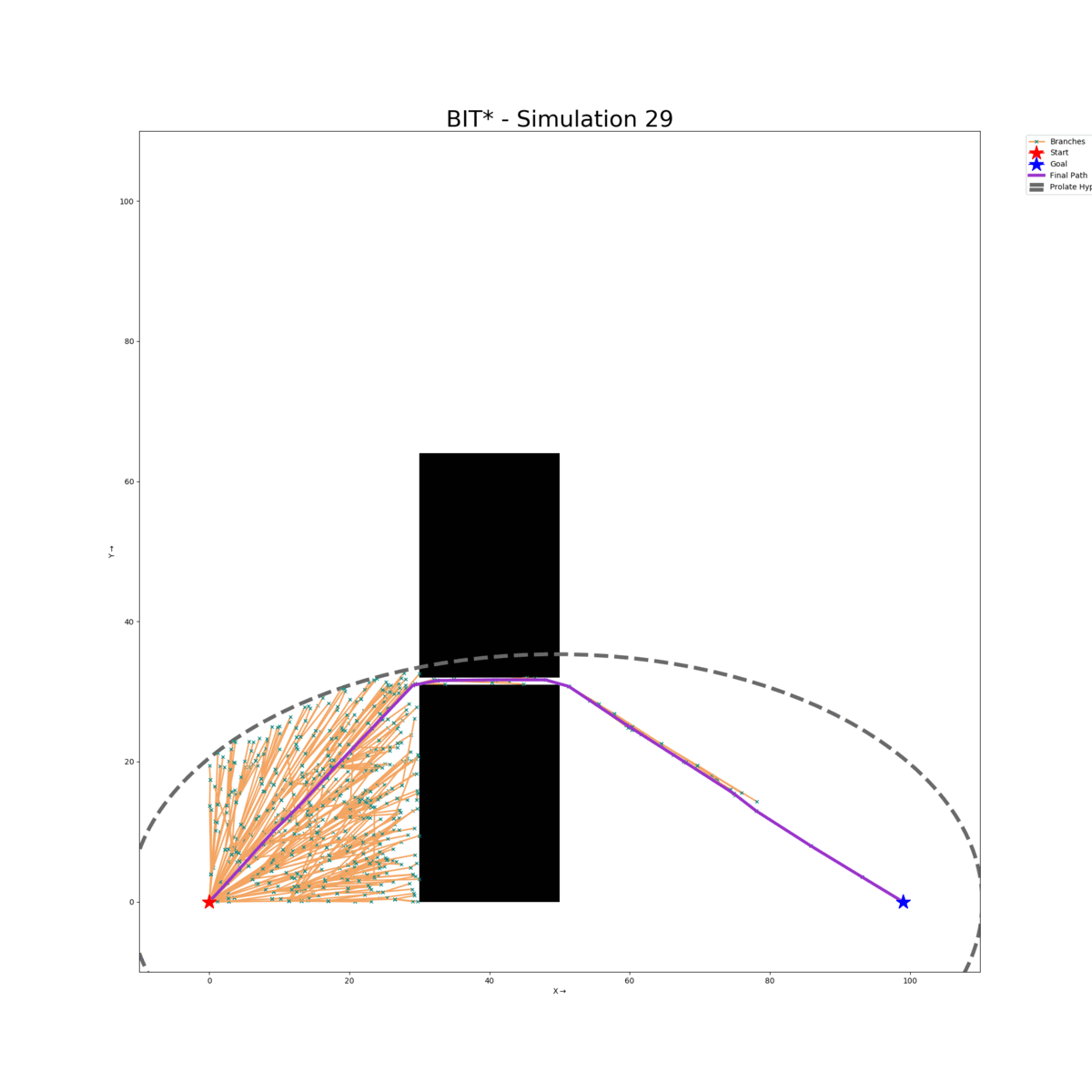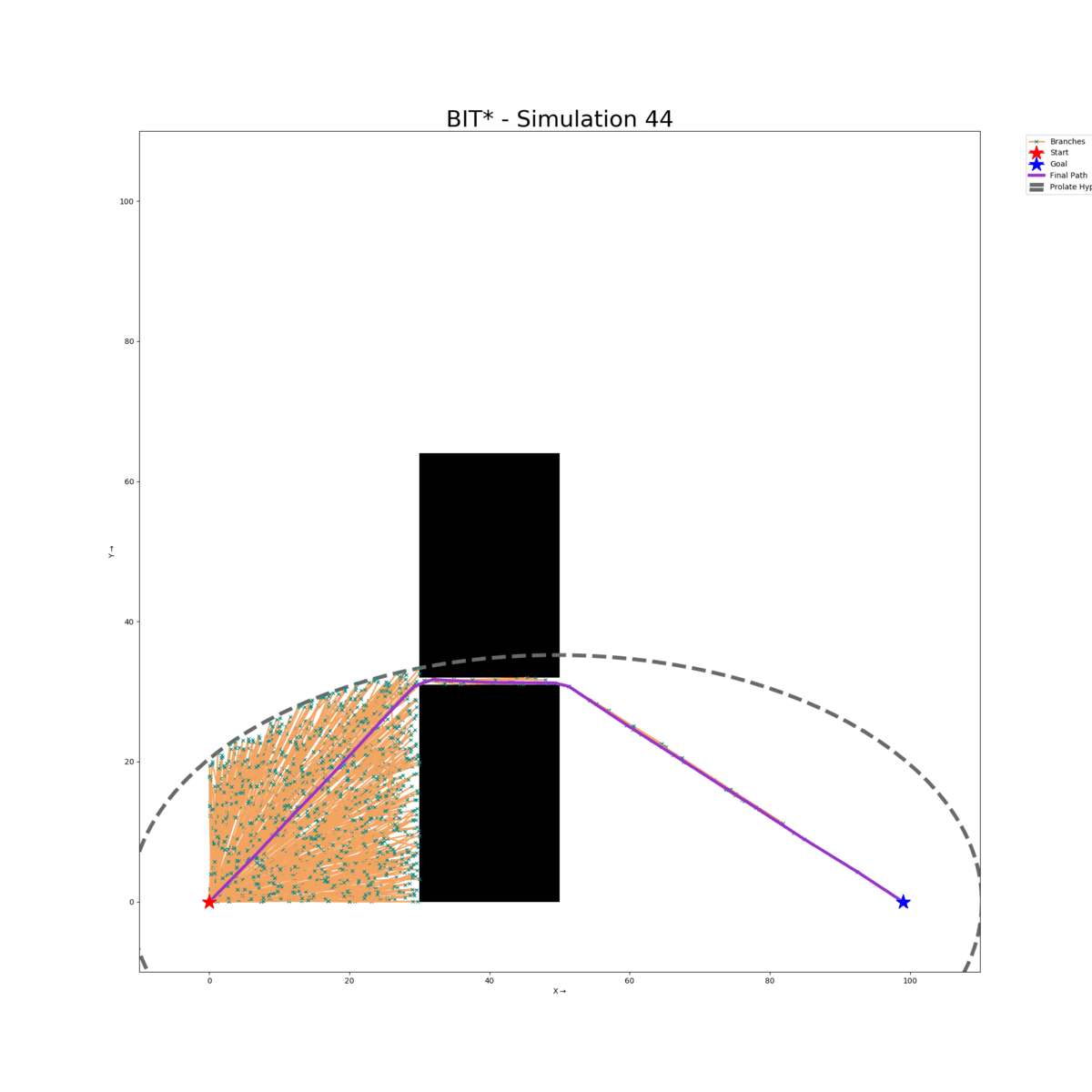
Introduction
Path Planning in Robotics has always relied on simple approximations to identify solutions. This is due to the difficulty to find one due to the high dimensional nature of the problem.
Generally, we can divide the approximations into 2 types:
- Search-based
- Sampling-based
Heuristics are used by search-based planners like A* to effectively search across graphs, but their efficiency is limited by the resolution of the selected approximation. To approximate the problem, sample-based planners such as RRT* employ random sampling. Here, the resolution can be increased until we find a suitable solution. These random samples approximate the region in all directions at the same time, making the search ineffective.
A recent approach called Batch Informed Trees (BIT*) combines the strengths of both search-based and sampling-based planners. In this work, we have used the pseudo-code from the paper and coded the algorithm from scratch, and tested its performance in ℝ2 space for different motion planning scenarios using a custom visualizer.
Installation
git clone https://github.com/Sahas-Ananth/BIT-Star.git
cd BIT-star
pip install -r requirements.txt
Usage
To use our python implementation of BIT-star, we provide a run.py file with options to specify all the arguments passed to the algorithm. A full list of options can be seen by running:
cd python
python3 run.py --helpExample Usage
To run BIT-star on a default map and only obtain the final path once the stop time has been reached, simply run:
python3 run.py --map_name Default --start 0 0 --goal 99 99 --seed 1 --stop_time 20To run BIT-star on a more complex map (Maze) and obtain visualizations once the stop time has been reached, run:
python3 run.py --map_name Default --start 0 0 --goal 99 99 --seed 1 --stop_time 20Results
Empty Map (Default)
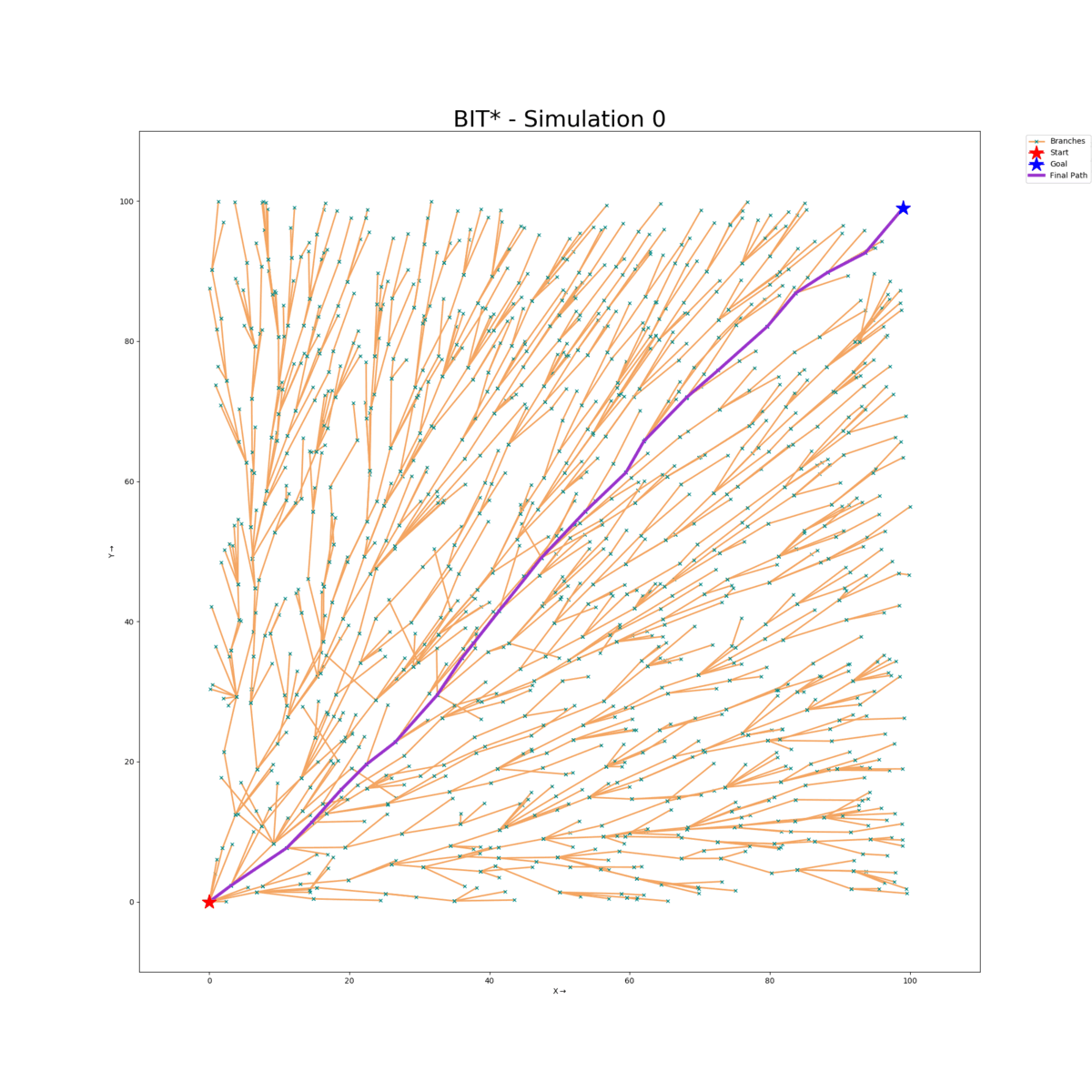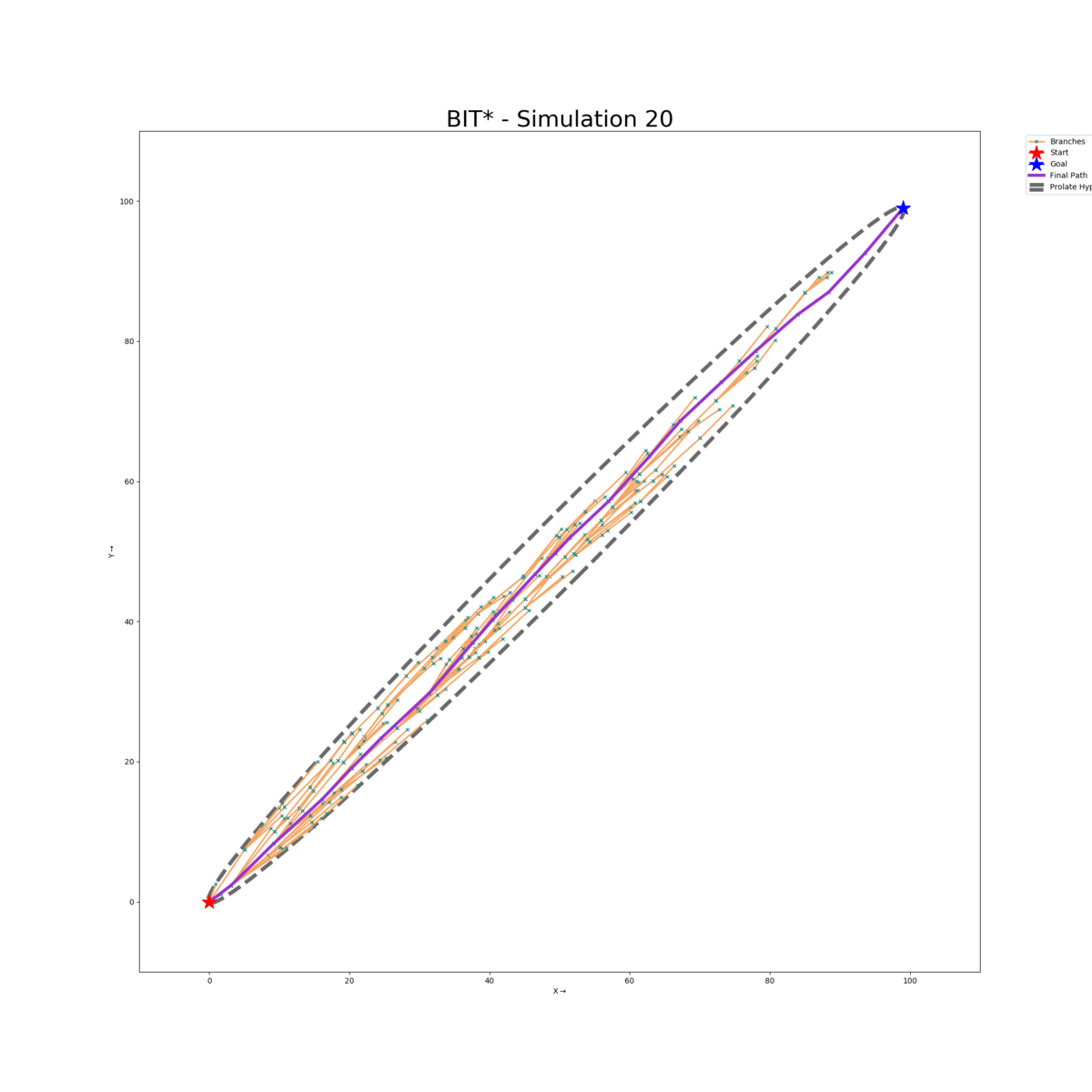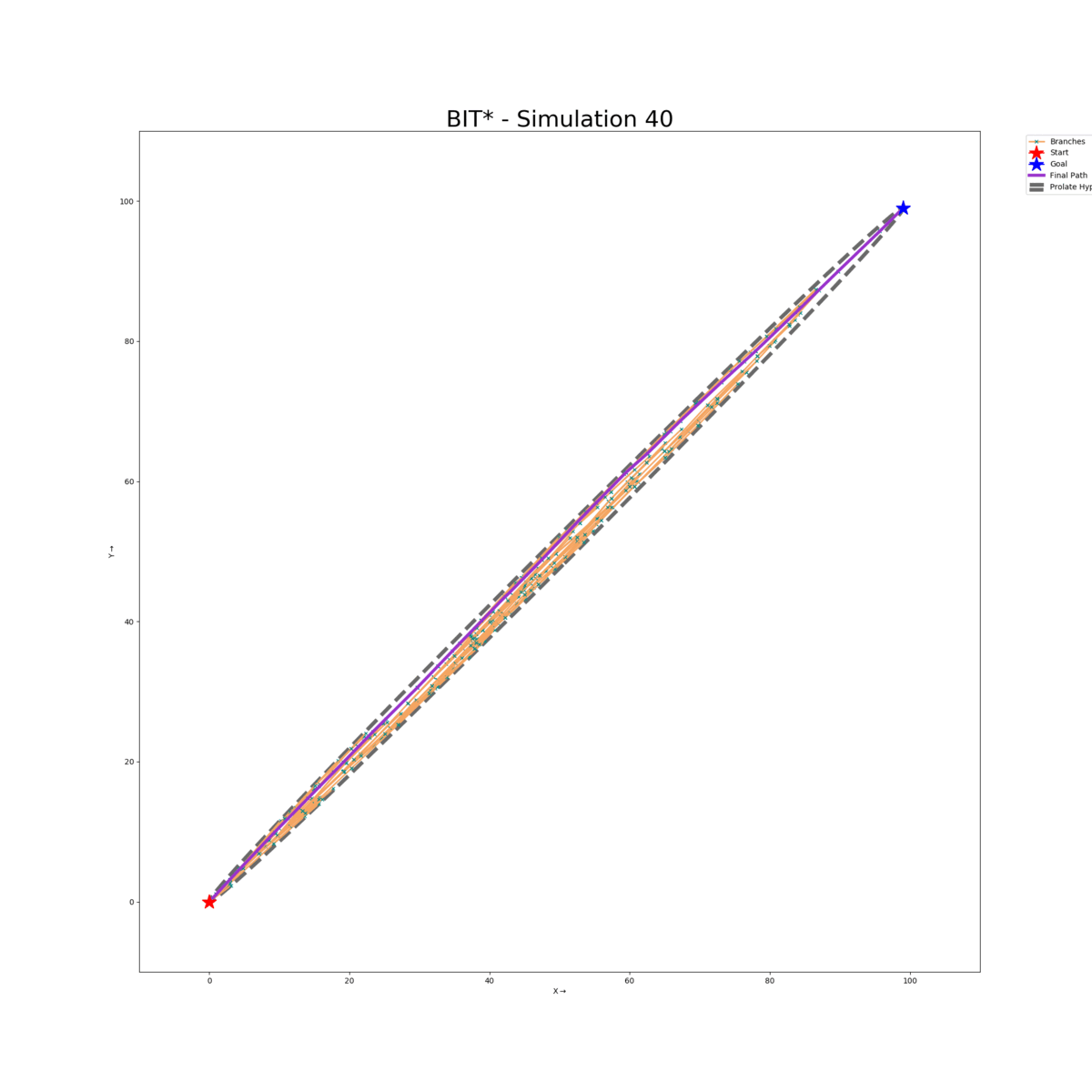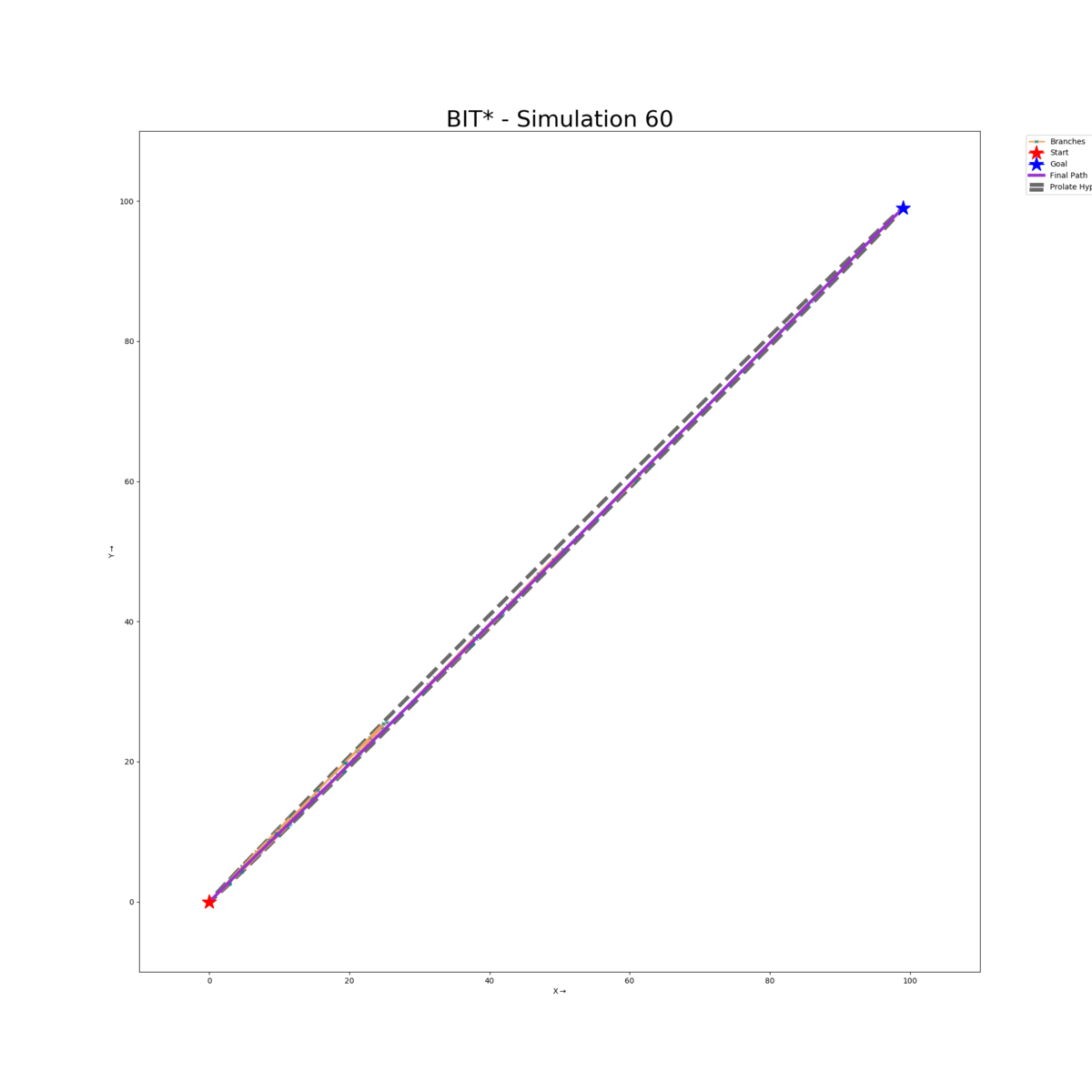
Enclosure Map
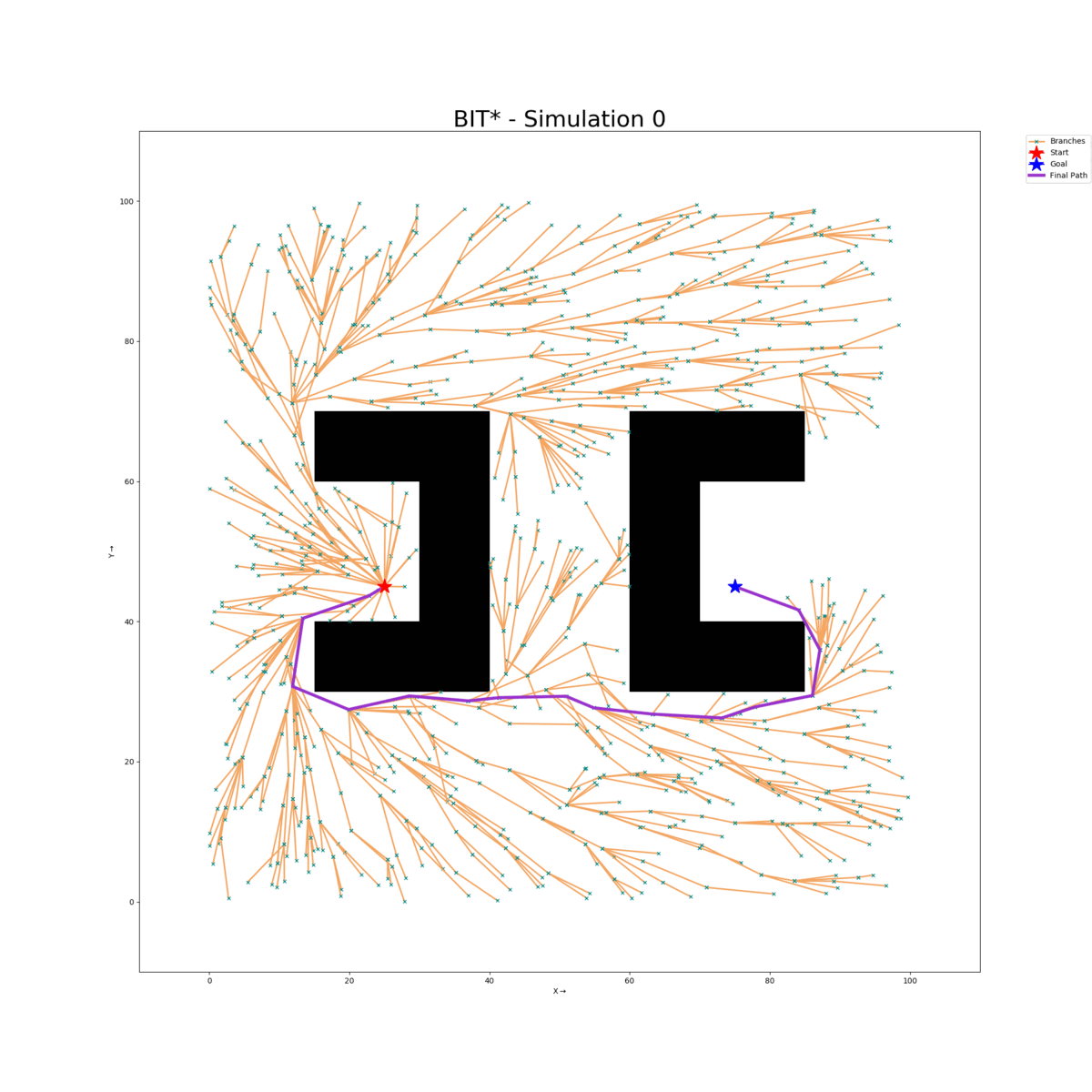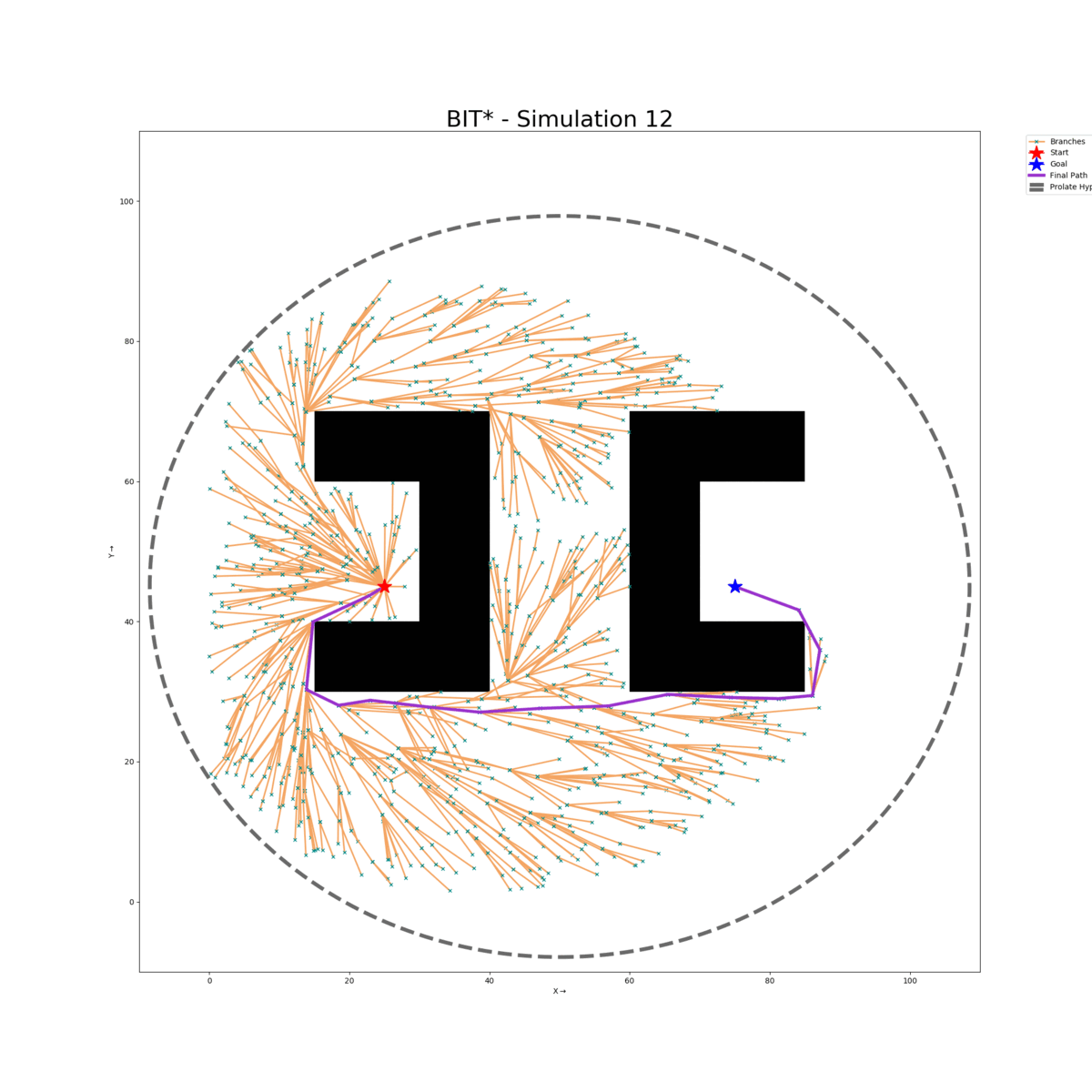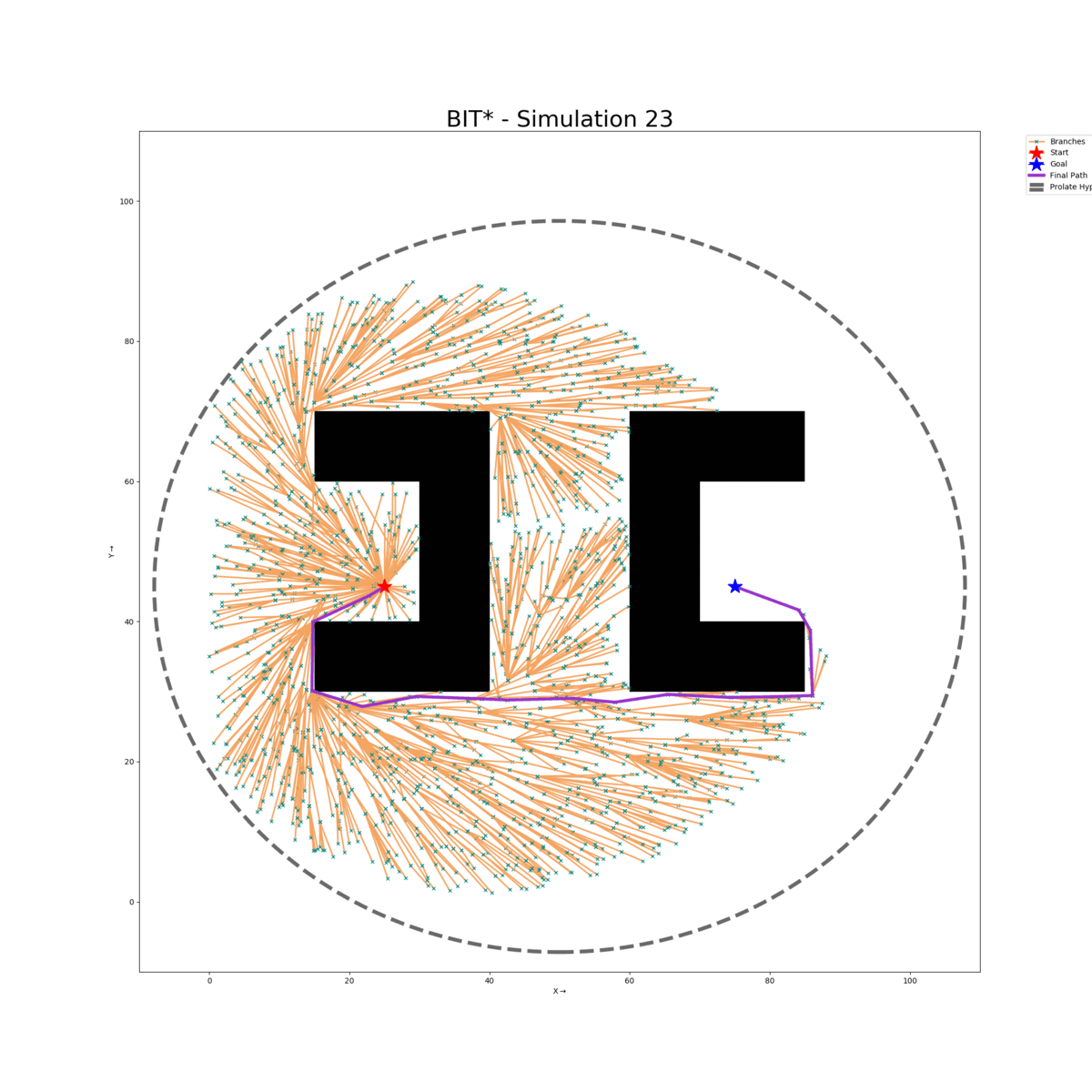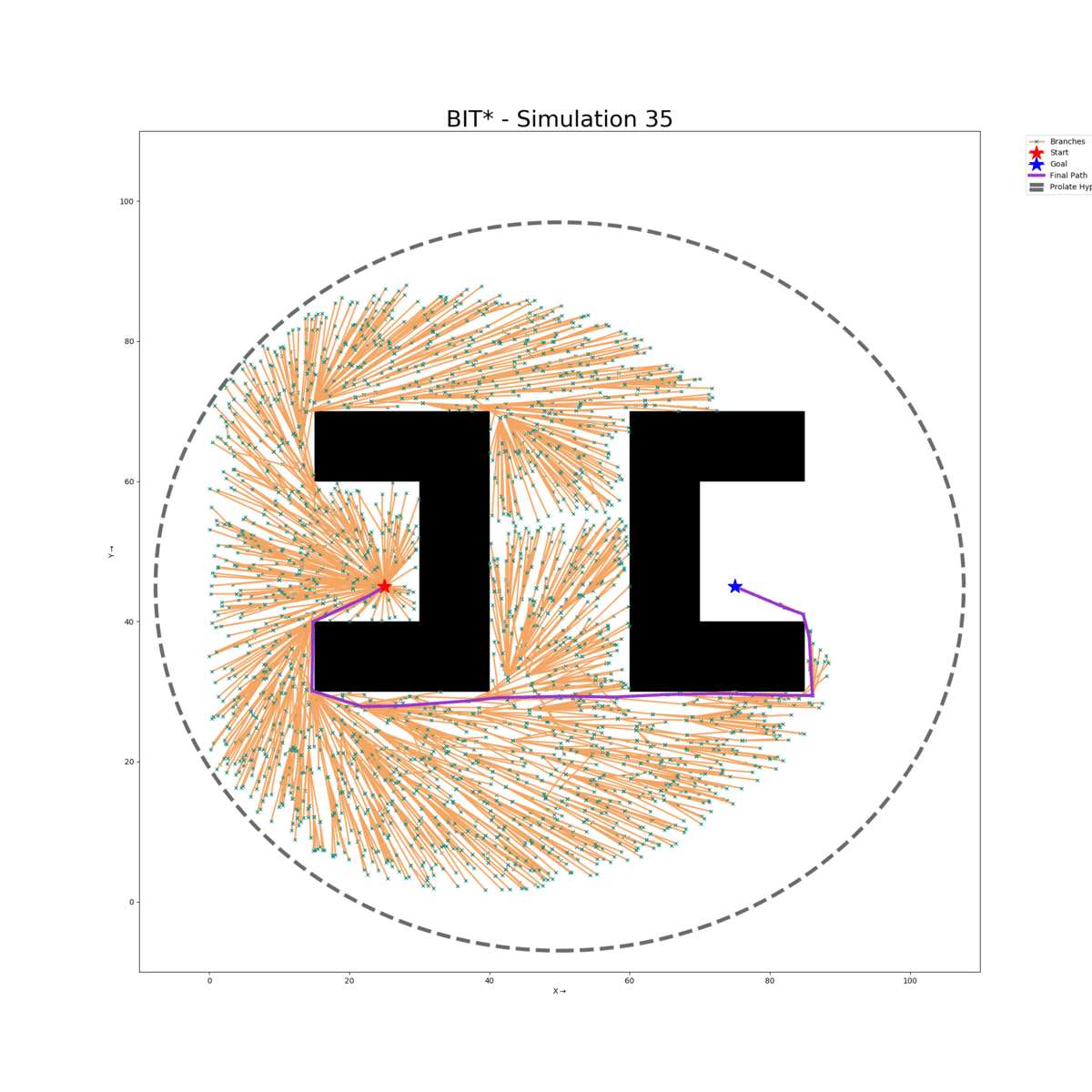
Maze Map
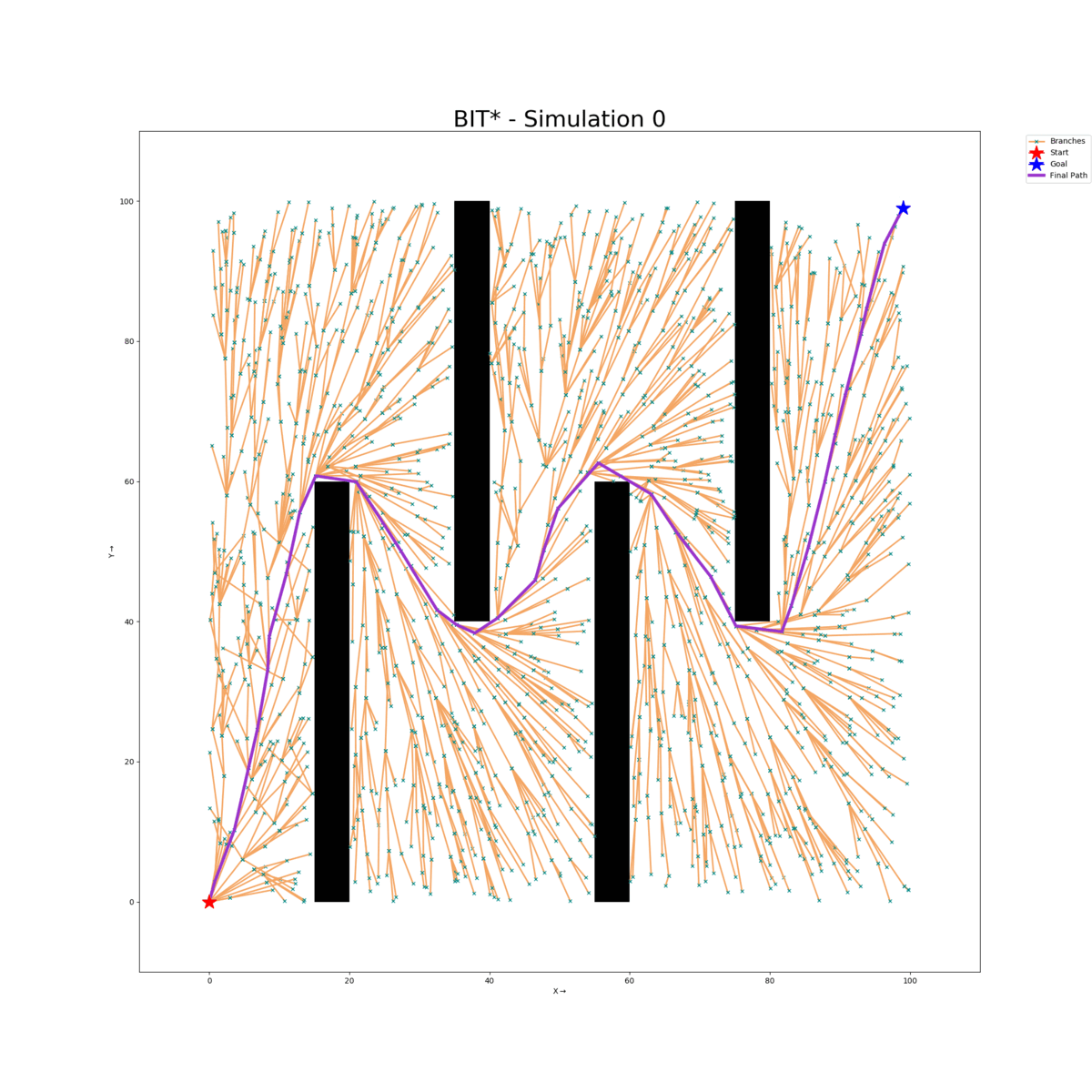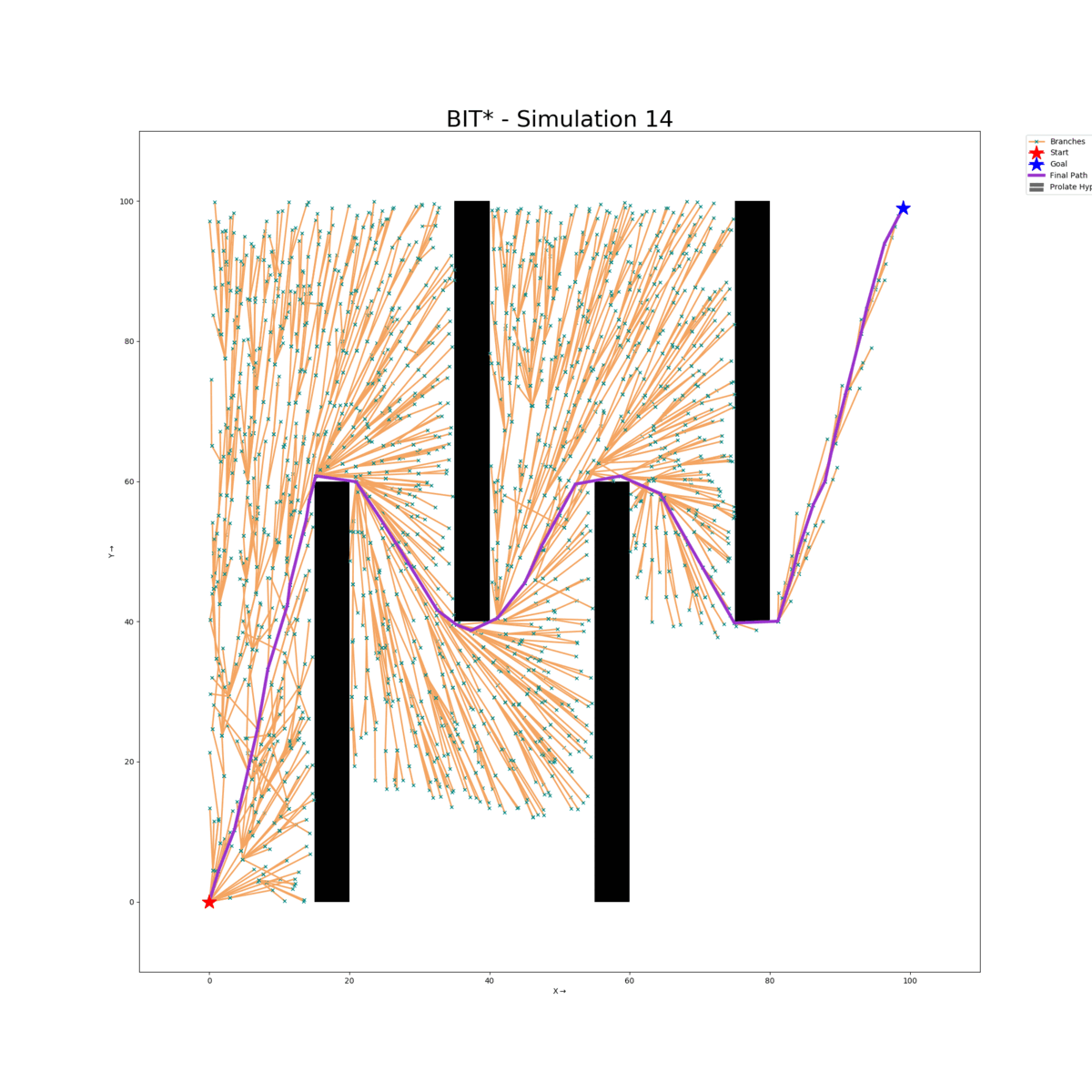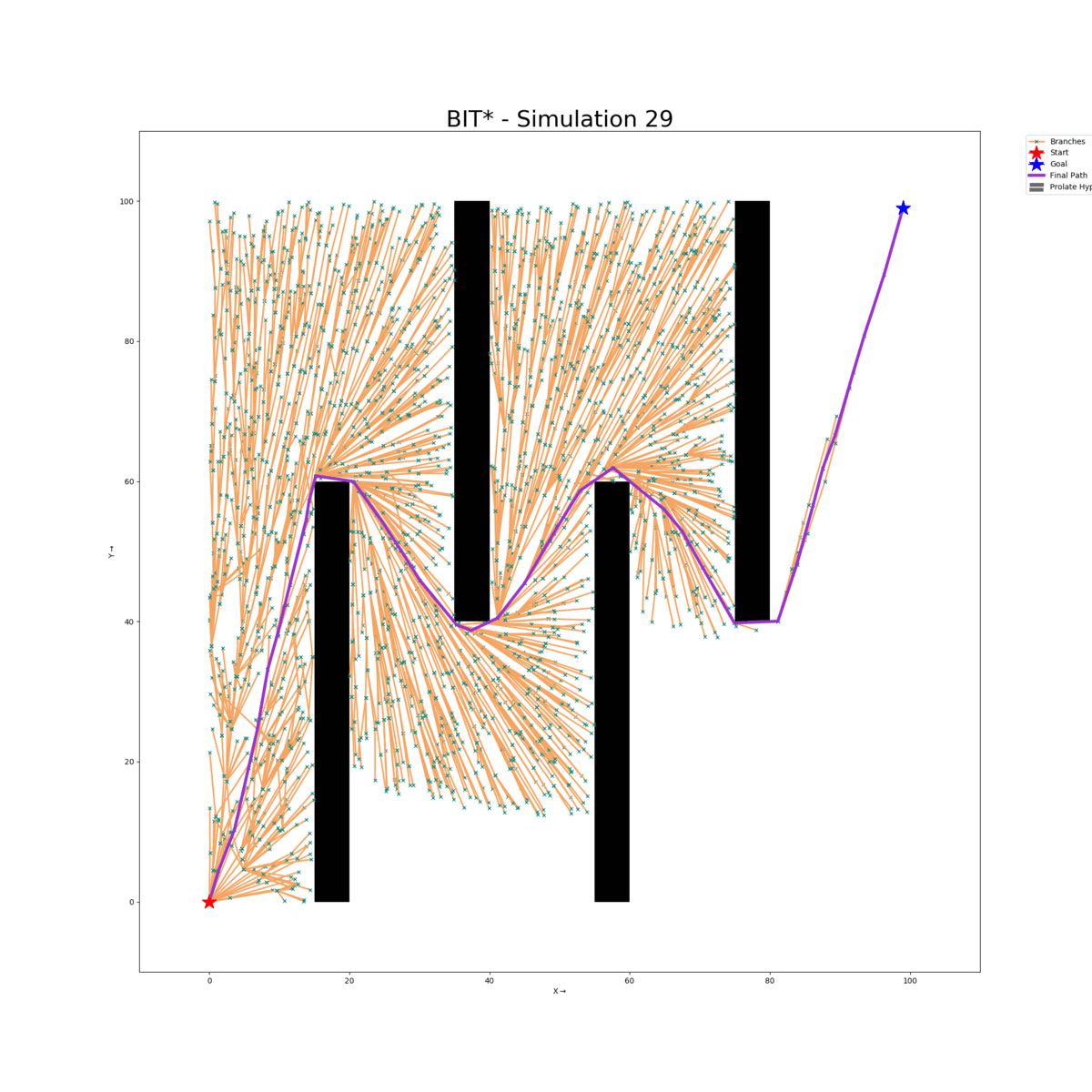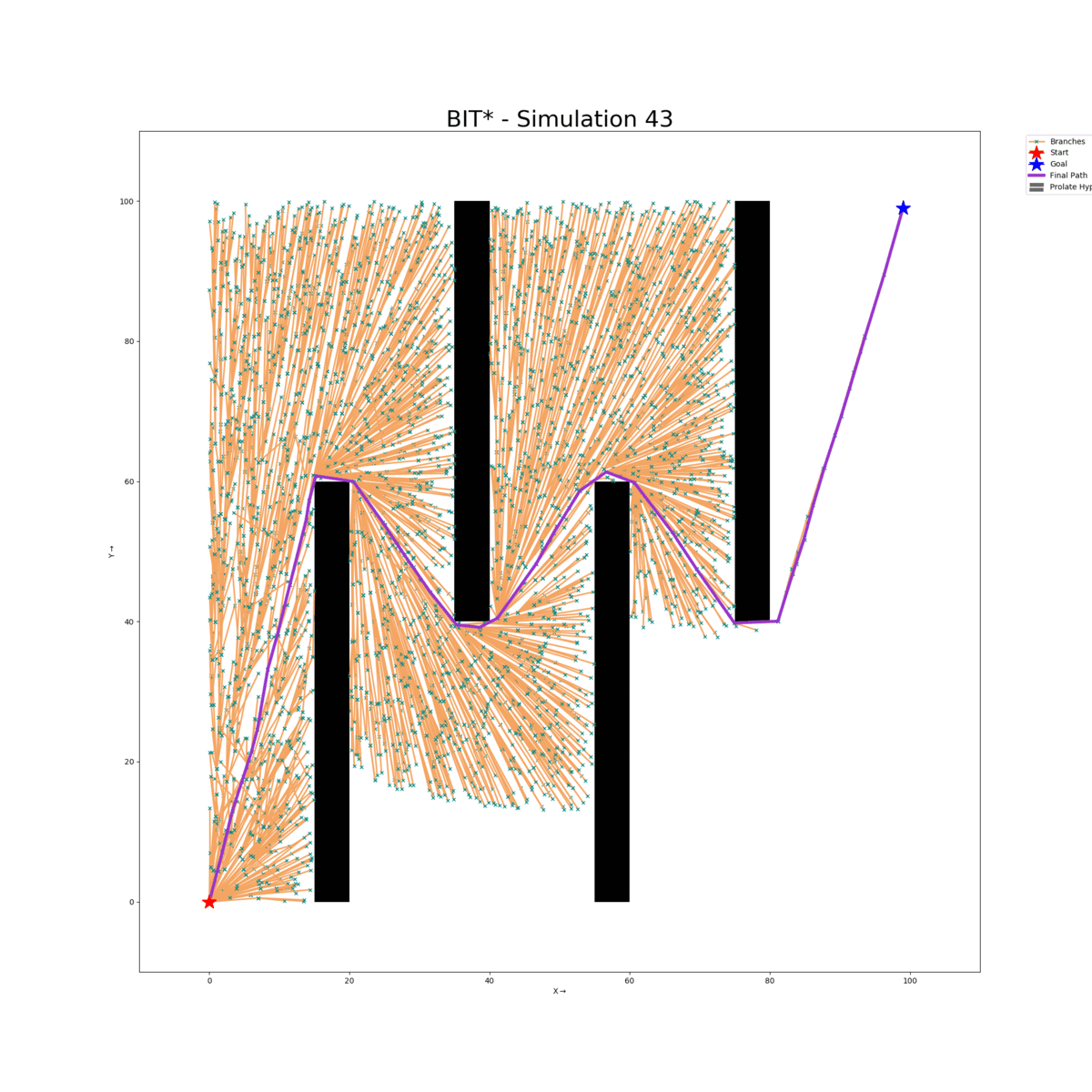
Wall Gap Map

